Curso de Cálculo Numérico

Professor Raymundo de Oliveira

| Home | Programa | Exercícios | Provas | Professor | Links |

Método dos Trapézios

Nesse método, dada a função a ser integrada, divide-se o intervalo de integração (a,b) em n partes iguais, sendo a amplitude h de cada intervalo igual a         h = ( b-a ) / n

Constrói-se a tabela de n+1 pontos (x_i , y_i ), i variando de 0 a n, onde x_i começa em a, valor inferior de X, indo até b, valor superior de X, e y_i corresponde a f(x_i).

Tem-se, assim, n intervalos e n + 1 pontos.

Ligam-se, por segmentos de reta, os pontos (x­_i , y_i) a (x­_i+1 , y_i+1), obtendo-se n trapézios.

A soma das áreas dos n trapézios será aproximadamente a área sob a curva, isto é, entre a curva e o eixo das abscissas (X).

Sendo assim, a soma das áreas dos trapézios nos dará uma aproximação da integral definida entre a e b.

Quanto maior o valor de n, isto é, o número de trapézios, melhor será a aproximação do valor da integral calculada.

.....

Pela figura acima, vê-se que a área de cada trapézio é dada por:

A_i = h.(y_i + y_i+1)/2 , isto é, altura vezes a base média.

Logo,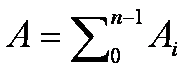
 a área total será dada por:

A = h (y₀ + y₁)/2 + h(y₁ + y₂)/2 + ... + h(y_n-1 + y_n)/2

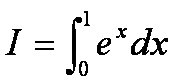
Vejamos um exemplo cujo resultado seja conhecido, para podermos analisar a aproximação, isto é, o erro ocorrido no cálculo da integral.

Sabemos que esta integral vale e –1 = 1,7182818284590...

Vamos calculá-la numericamente, trabalhando com 3 casas decimais..

Tomemos n = 2 como sendo o número de divisões do intervalo [0 , 1].

Assim, h = (1-0)/2 = 0,5 .

Vamos construir a tabela (x,y).

I » A = 0,5 (1,000/2 + 1,649 + 2,718/2) = 1,754

Como já sabemos o valor exato da integral, o que não acontecerá normalmente, podemos calcular o erro cometido:

e = 1,718 – 1,754 = - 0,036

O erro negativo está indicando que a área calculada pelo Método dos Trapézios é maior que o valor da integral. (figura a seguir)

...

Isso já era esperado, pois a concavidade da curva é para cima, o que faz com que a área dos trapézios sejam maiores que os valores das áreas sob a curva.

Assim, quando f^” (x) > 0, isto é, concavidade para cima, a área calculada pelo Método dos Trapézios é maior que o valor da integral.

Por outro lado, se f^” (x) < 0, isto é, concavidade para baixo, a área calculada pelo Método dos Trapézios é menor que o valor da integral. (referência ao lado)

De fato, pode-se demonstrar, veja bibliografia anexa, que o erro cometido quando se calcula uma integral pelo Método dos Trapézios é dada por:

e = I – A = - (b-a) h² f ^”(ε)/12 , onde   a < ε < b .

Sendo h = (b-a) / n , pode-se escrever o erro como sendo:

e = - (b-a)³ . f ^”(ε) / (12.n²)

Em geral, estamos interessado na ordem de grandeza do valor absoluto do erro e não se ele é positivo ou negativo. Assim,

| e | = (b-a) . h² . |f ^”(ε)|/12 ou (b-a) . |f ^”(ε)| / (12.n²)

Estimando-se o maior valor que |f ^”(ε)| pode ter no intervalo (a,b), pode-se obter o maior valor que o erro pode ter, estimando-se, assim, a precisão do cálculo da integral.

Cota Superior do Erro é esse valor que o erro não ultrapassa, em módulo.

Quando nos referirmos a erro, e, estaremos nos referindo ao seu valor absoluto, a menos que indicado.

Vejamos o cálculo do maior erro possível, no exemplo recém calculado.

f(x) = e^x , donde f ^’(x) = e^x  e f  ^”(x) = e^x .

No intervalo (0,1), podemos afirmar que e^ε < e = 2,7183 .

Logo o erro será inferior a:

e < (1-0).0,5². 2,7183/12 = 0,057

De fato, o erro é inferior, como já vimos: e ~ 0,036 . A razão de a estimativa ter sido maior é a de que tomou-se, como segunda derivada, o maior valor possível, que era o do final do intervalo (0,1).

Vamos repetir o cálculo dessa mesma integral anterior, tomando-se n = 4, isto é, dobrando-se o valor de n e obtendo-se, logicamente, um valor mais aproximado da integral, com erro menor.

I » A = 0,25 (1,000/2 + 1,284 + 1,649 + 2,117 + 2,718/2) = 1,727

Nesse caso, o erro será:

e = 1,718 – 1,727 = - 0,009

Veja que, dobrando-se o n, o erro caiu cerca de 4 vezes, o que era de se esperar, pois o erro é, aproximadamente, inversamente proporcional ao quadrado de n.

O aproximadamente deve-se a que, na expressão do erro aparece um ε que está entre a e b, mas que varia quando n se altera, não ficando necessariamente constante.

Daí poder-se afirmar que o erro é aproximadamente proporcional ao inverso do quadrado de n.

 Se você tiver dúvidas sobre a matéria, meu e-mail é: raymundo.oliveira@terra.com.br